Vamos tentar aqui explicar porque George Boole é muito mais importante que a busca do Google e como o Google usa também outros conceitos computacionais.

Por Matheus Gonçalves

Hoje alguns sites que eu considero muito importantes e confiáveis começaram a divulgar o novo doodle do Google, homenageando o aniversário de 200 ano de George Boole. Toda homenagem a ele é muito bem vinda, afinal Boole foi um matemático brilhante, criador de um conceito básico de qualquer computador que existe hoje em dia.

Este é o Doodle:

 

 

Acontece que alguns destes sites, como a gigante BBC, estão informando seus leitores da seguinte forma:

 

 

Poxa, eu entendo que álgebra booleana é um assunto meio espinhoso e é necessário dar uma mastigada pra ficar mais didático. Entendo também que eles quiseram fazer um link entre o doodle do Google e sua ferramenta de busca. Mas do jeito que foi colocado, ficou parecendo que Boole inventou a fórmula do Google (o que não é verdade) e que ele só é importante por isso.
 
Álgebra Booleana existe em todos os computadores, em software e hardware

Eu não vou entrar aqui nos detalhes de quem foi o matemático inglês George Boole. Existe muita coisa online sobre ele.

Em vez disso, o meu foco será tentar complementar o trabalho da BBC sobre o assunto, me aprofundando um pouco mais e fazer aqui o que talvez não fosse possível fazer lá.

Por exemplo, precisamos citar que o conceito de álgebra booleana foi criado em meados de 1854, como uma forma revolucionária de pensar, não só para lógica, mas também para engenharia e ciências da computação.

Sim, circuitos eletrônicos. Placas, portas digitais. Aquelas coisas que parecem cidadezinhas em miniatura dentro do computador ou rádio que você algum dia deve ter aberto e tomou bronca de algum adulto. Ou quando você estava tentando montar algum computador, placa mãe, placa de vídeo, aquela coisa toda.
 

 
Computadores trabalham com 0 e 1. Mas como manipular isso?

Vou tentar mostrar alguns conceitos de eletrônica aqui, mas não se assuste se não entender muito bem. A ideia é mostrar que isso está presente num microcontrolador, no hardware de um equipamento eletrônico.

Veja a imagem abaixo (publicada pelo All About Circuits), e tente enxergar como se fossem interruptores ligados a uma lâmpada. Dependendo do que você fizer com os interruptores, quais você ligar ou não, a lâmpada pode ou não acender.

 

 

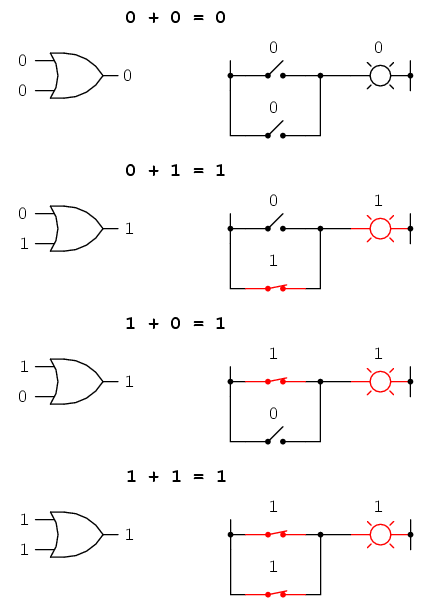
Essa coisa que parece uma ponta de flecha é uma porta OR (OU). Para que o resultado seja igual a 1 (luz acesa), OU uma entrada precisa ser igual a 1, OU a outra entrada precisa ser igual a 1. Por isso que quase todas as lâmpadas estão acesas.

Existem outros tipos de portas, como portas AND (E), que precisam que uma entrada E outra entrada sejam igual a 1 ao mesmo tempo para dar um sinal de saída igual a 1 e acender a lâmpada.

 

 

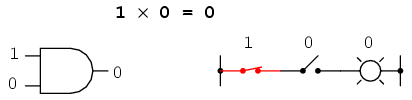
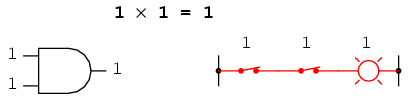
Uma vez que você aprende como essas portas funcionam, você consegue ir manipulando as entradas e saídas com sinais, obtendo o resultado que você procura, para, por exemplo, exibir um resultado de uma soma, ou mostrar caracteres em um display eletrônico.

Essa fórmula também pode ser explicada mais tecnicamente da seguinte maneira:

• Você começa com uma ideia de que alguma declaração de entrada E é verdadeira ou falsa. Não pode ser nada entre verdadeiro ou falso.
• Com isso, você pode formar outras declarações de saída S, que podem ser também verdadeiras ou falsas, combinando as declarações de entrada E em conjunto, utilizando operadores fundamentais AND, OR e NOT.

Isso me lembra minhas aulas de técnicas digitais na faculdade. Era bem divertido ficar brincando de atendente do PABX (pergunte pros seus pais).
 

 
Ou seja, essa álgebra booleana permitiu que, com cruzamentos bem mais complexos, conseguíssemos manipular sinais digitais e eventualmente chegamos a como os computadores funcionam atualmente.
 
E como esse conceito de lógica funciona no software?

De forma geral, qualquer programa de computador que faça a verificação de duas variáveis, dentro de um conceito lógico binário, também está utilizando álgebra binária.

Imagine um jogo ou qualquer sistema de cadastro que mostre uma lista de cidades baseado em parâmetros de entrada. Como, por exemplo, um país e um CEP.

Se o sistema for bem feito, o país e o CEP serão utilizados para criar os sinais de entrada. Para cada vez que, na lista de cidades, o país e o CEP forem iguais aos que você escolheu, o sistema vai retornar 1 e adicionar aquela cidade à lista para exibir pra você no final da consulta.

 

 
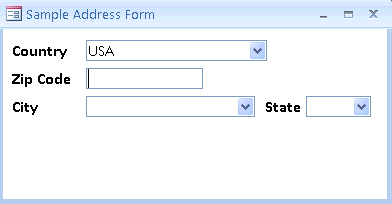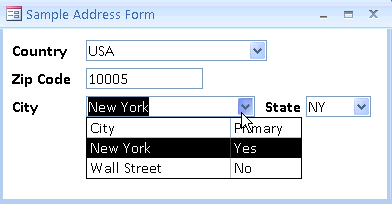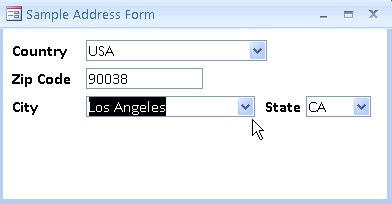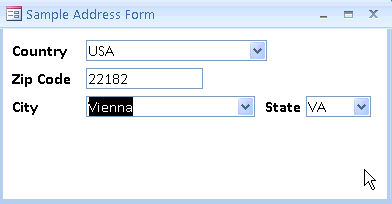
E operações lógicas assim acontecem em praticamente qualquer programa ou aplicativo, não só para cadastros, mas para tomadas de decisão ou operações triviais.

Portanto, o que Boole criou está presente nas buscas do Google porque existe em quase qualquer computador e quase qualquer software.
 
E como funciona o algorítimo do Google então?

Essa é uma pergunta de US$ 1 milhão. Além de usar lógica e álgebra booleana em seus robozinhos e servidores, a gente imagina que a empresa também use sistemas avançadíssimos de indexação feita com o Googlebot, que determina a frequência com que visita uma página segundo uma série de fatores, como sua importância, número de acessos.

Isso sem contar algum tipo de busca vertical e horizontal, programadas em casa e das quais nós reles mortais nunca vimos o código (talvez aplicando grafos), que consegue cruzar essas informações e dar uma resposta ao usuário em segundos.
 

 
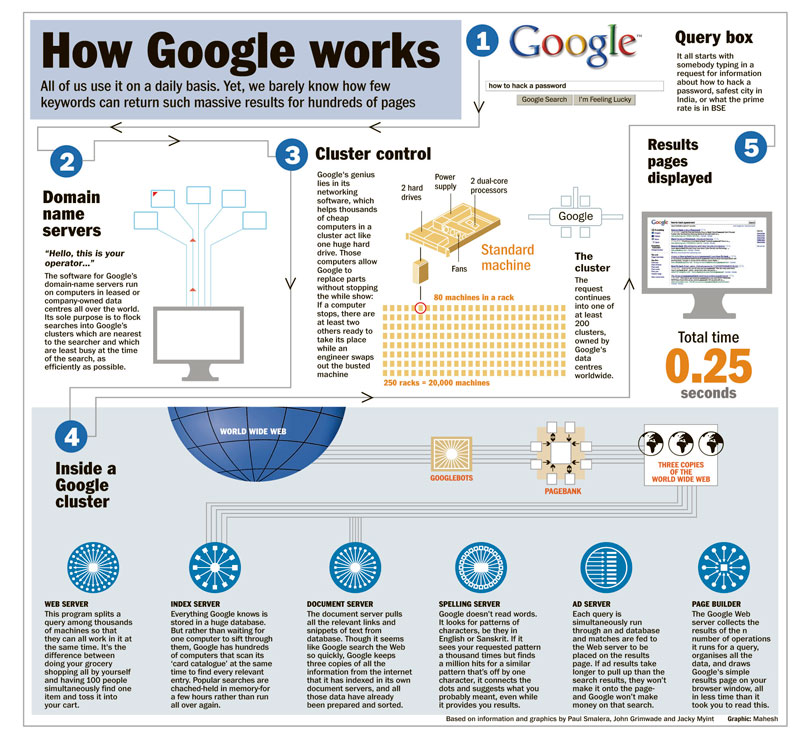
Na soma dos fatores…

Dá pra se aprofundar muito na arquitetura do Google, mas isso fica pra outro post. O que eu queria evidenciar é que:

A Lógica e a Álgebra criada por George Boole são usadas em muito mais que o Google, e que o Google usa muito mais que esses conceitos booleanos em seus sistemas. Espero que a magnitude destas diferenças tenha ficado clara.

Mas como esses são assuntos que podem ser complementados com outros detalhes, não fique tímido e colabore com o post aqui embaixo na área de comentários. Aqui no TOAD nossa relação com o leitor é AND, e não NOT.

Let’s discuss.

BBC, Boole, Correção, didática, Doodle, featured, George Boole, Google, lógica, Lógica Booleana, Números binários

---